[CompPhys]
CP-Home Vorherige Ü 6. Übung Nächste Ü
  1. Monte-Carlo-Simulation des 2D Ising Modells

    • Das ferromagnetische Ising Modell wird durch den Hamiltonian
      displaymath7
      beschrieben, wobei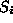 tex2html_wrap_inline36 die Werte +1 und -1 annehmen kann.

    • In mehr als einer Raumdimension zeigt das Modell bei einer endlichen kritischen Temperatur einen Phasenübergang zu einer ferromagnetisch geordneten Phase. In zwei Dimensionen kann das Modell exakt gelöst werden (Onsager 1944; siehe z.B. K. Huang, Statistical Mechanics), es ergibt sich
      displaymath10

    • Bei der Simulation mit Hilfe des Metropolis Algorithmus wird als Übergangswahrscheinlichkeit von einem Zustand S zu einem Zustand S'
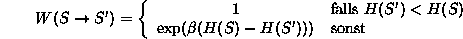
      displaymath14
      benutzt.

      ising.c | ising2.c

  2. Problem des Handlungsreisenden und Simulated Annealing

    • Das Problem des Handlungsreisenden besteht darin, eine Rundreise durch N Städte mit möglichst kurzer Wegstrecke zu planen. Dabei soll jede Stadt genau einmal besucht werden.

    • Der Hamilton-Funktion entspricht hier die Weglänge. Wie oben kann eine Übergangswahrscheinlichkeit von einer alten zu einer neuen Rundreise mit Hilfe eines Boltzmann-Gewichts definiert werden. Numerisch schneller ist aber unter Umständen
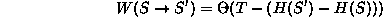
      displaymath23

    • Zur Bestimmung einer optimalen Rundreise wird das System ausgehend von hoher Temperatur langsam abgekühlt (Simulated Annealing). Man hofft, dadurch in einem Zustand nahe am Grundzustand (optimaler Weg) zu enden.

      travel.c | travelf.c | tsp.nb

      TSPLIB - a library of sample instances for the TSP
      Concorde - a code for solving Traveling Salesman Problems

Zuletzt verändert: Alex Weiße