In den bisher untersuchten Beispiel-Programmen wurde kaum Rücksicht auf die zur Rechnung benutzte Hardware genommen. In der Praxis spielt jedoch die Architektur eines Rechners eine große Rolle und geschickte Programmierung kann die zur Lösung eines Problems benötigte Rechenzeit deutlich verkürzen.

• C versus Fortran

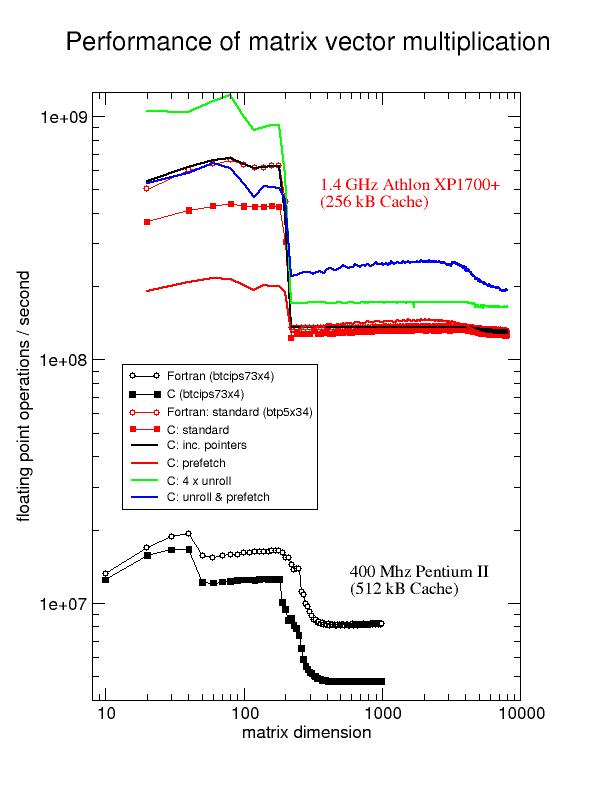
  Obwohl moderne Compiler sehr weit entwickelt sind und eine Vielfalt an Methoden zur Code-Optimierung beherrschen, gilt nach wie vor, daß Fortran-Programme meist wesentlich schneller als äquivalente C-Programme sind. Als Beispiel wird die in vielen numerischen Simulationen auftauchende Multiplikation zweier Matrizen, C = C + A*B, untersucht.

  muma.c | muma.f

• Cache/Memory Access

  Dank hoher Taktraten und entsprechender Architektur sind moderne CPUs sind in der Lage, riesige Datenmengen innerhalb weniger Taktzyklen zu verarbeiten. Zum Problem wird deshalb häufig die schnelle Bereitstellung dieser Datenmengen. Bei den meisten aktuellen Rechnern ist dem Hauptspeicher ein wesentlich schnellerer Speicherbereich, der Cache, vorgeschaltet. Dieser erkennt und puffert häufig benutzte Daten, so daß sie der CPU schnell zur Verfügung stehen. Ungünstige Programmierung (schlecht verteilte Daten) oder auch eine große Menge zu verarbeitender Daten überfordern jedoch leicht den Cache.

  Anhand von Matrix-Matrix- und Matrix-Vektor-Multiplikation soll der Einfluß von Schleifenanordnung und Datenmenge auf die Programm-Performance untersucht werden.

  mult_matrix.c
  mvmtime.c | mvmloop.f

• Codeoptimierung

  Durch erhöhten Programmieraufwand können auch C-Programme maximale Performance erzielen. Der hier vorgestellte Code illustriert die Techniken loop-unrolling und prefetching, die insbesondere für PCs nützlich sind.

  mvmtimeO.c

• Diskretisierte Felder / finite Differenzen

  Um kontinuierliche Probleme numerisch zu Behandeln ist meist eine geeignete diskrete Formulierung erforderlich. Aus einem physikalischen Feld wird so ein Satz von Feldwerten an verschiedenen Punkten, aus einer Ableitung des Feldes wird eine Differenz zwischen Werten des Feldes an benachbarten Punkten etc. In der Übung werden die einfachsten Diskretisierungsschemen vorgestellt.

• Iterative Lösung statischer Probleme

  Laplace-Gl. mit verschiedenen Randbedingungen, Schrittweiten, ...

  laplace1.c | laplace2.c | plot4c.gnu

• Integration zeitabhängiger PDGln.

  Wärmeleitungsgleichung

  eqheat.c

  Wellengleichung

  eqstring.c

  Korteweg - de Vries Gleichung

  soliton.c

  Schrödingergleichung

  schroed.c