[CompPhys]
CP-Home Vorherige Ü 10. Übung Nächste Ü
  1. Assoziativer Speicher

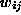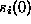    • Das von Hopfield und Little vorgeschlagene Modell eines assoziativen Speichers besteht aus einem Satz von N Neuronen, die untereinander durch Synapsen tex2html_wrap_inline50 verbunden sind. Werden die Neuronen zum Zeitpunkt t=0 mit einem Muster tex2html_wrap_inline54 initialisiert, so soll das Netzwerk unter der Dynamik
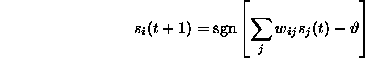
      displaymath8
      zu einem Fixpunkt konvergieren, der dem vorher gespeicherten Muster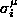 tex2html_wrap_inline56 mit der größten Ähnlichkeit zum Muster 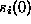tex2html_wrap_inline54 entspricht. Ausgehend von einer unscharfen Eingabe, soll sich das Netz also an ein gespeichertes Muster erinnern. Zum Training des Netzwerks werden in der Übung die Algorithmen von Hebb, Diederich/Opper und Krauth/Mézard benutzt.

    • Hebbsche Regel: Die Kopplungsstärken ergeben sich aus
      displaymath13
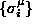      wobei tex2html_wrap_inline60 die M zu speichernden Muster bezeichnen.

    • Algorithmus von Diederich und Opper: Die Kopplungsstärken ergeben sich iterativ aus
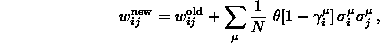
      displaymath20
      wobei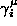 tex2html_wrap_inline64 den Stabilitätskoeffizienten des Musters 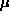tex2html_wrap_inline66 bezeichnet,
      displaymath29
      Konvergenz ist erreicht, wenn keine Kopplung mehr verändert wird.

    • Algorithmus von Krauth und Mézard: Für jedes Neuron i wird jeweils das Muster mit der geringsten Stabilität verstärkt, d.h.
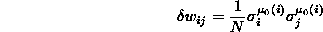
      displaymath33
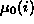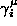      wobei tex2html_wrap_inline70 das Muster mit dem kleinsten Stabilitätskoeffizienten tex2html_wrap_inline64 bezeichnet. Konvergenz ist erreicht, wenn die Stabilität aller Muster einen gegebenen positiven Wert überschreitet.

      assmem.c
      boldlett.pat | thinlett.pat | boldnum.pat

  2. Graded Neurons

    • Mit Hilfe vektorwertiger Neuronen soll das Problem des Handelsreisenden gelöst werden. Dazu wird jede Stadt durch ein Neuron 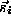tex2html_wrap_inline74 beschrieben, dessen Ausgabewert ein Einheitsvektor im N dimensionalen Raum ist. Die Richtung dieses Vektors gibt an, wann die Stadt i während der Rundreise besucht wird.

    • Das Problem wird mit dieser Notation auf ein sog. Potts Modell abgebildet, dessen Grundzustand gesucht ist. Wie in der Vorlesung erläutert, werden im vorliegenden Program die mean-field Gleichungen zum Modell iterativ gelöst und langsam die Temperatur abgesenkt (vergl. Simulated Annealing, 6. Übung).

      tsppotts.c

Zuletzt verändert: Alex Weiße