
![[CompPhys]](compphys.gif)
| CP-Home | Vorherige Ü | 2. Übung | Nächste Ü |
- Euler-Maclaurin-Formeln
- Für eine im Intervall [0,1] 2n-mal stetig
differenzierbare Funktion f(x) und eine Konstante
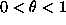 gilt:
gilt:
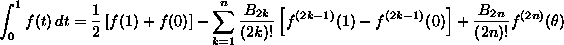
wobei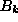 die Bernoulli-Zahlen bezeichnet. Wendet man diese
Formel auf ein in m gleichgroße Teilintervalle
zerlegtes Integral über [a,b] an, findet man
die Bernoulli-Zahlen bezeichnet. Wendet man diese
Formel auf ein in m gleichgroße Teilintervalle
zerlegtes Integral über [a,b] an, findet man
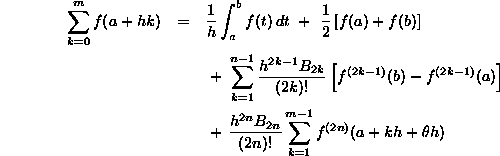
wobei h = (b-a)/m. - Die letzte Formel kann zu einer sehr genauen Abschätzung höherer Terme in einer unendlichen Summe benutzt werden.
- Für eine im Intervall [0,1] 2n-mal stetig
differenzierbare Funktion f(x) und eine Konstante
- Integration
- Prinzip aller Integration ist eine Schätzung
der Form
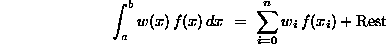
- Eine Schätzung
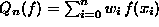 heißt
Interpolations-Quadraturformel, wenn
sie für Polynome bis zum
Grade n exakt ist (d.h. der Rest ist Null).
Zu vorgegebenen Stützstellen xi
existiert genau eine solche Formel. Es gilt
heißt
Interpolations-Quadraturformel, wenn
sie für Polynome bis zum
Grade n exakt ist (d.h. der Rest ist Null).
Zu vorgegebenen Stützstellen xi
existiert genau eine solche Formel. Es gilt
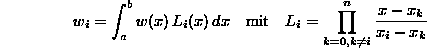
wobei w(x) eine beliebige Gewichtsfunktion und Li(x) die Lagrangeschen Interpolationspolynome bezeichnen. - Interpolations-Quadraturformeln mit
äquidistanten Stützstellen
heißen Newton-Cotes-Formeln.
- Beispiel: Bei der Trapezregel werden im
Intervall [0,1] die Stützstellen
x0 = 0 und x1 = 1
gewählt. Die Gewichte
ergeben sich für w(x)=1 zu
w0 = w1 = 1/2, also
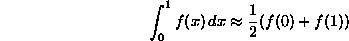
- Eine Schätzung
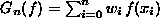 ist vom Gaußschen Typ, wenn sie
für Polynome bis zum Grade 2n+1 exakt ist.
Zu vorgegebener Gewichtsfunktion w(x)
gibt es genau eine Gaußsche Quadraturformel.
Dabei sind die Stützstellen nicht mehr
frei wählbar, sondern durch die Nullstellen
des (n+1)-ten, bezüglich w(x) orthogonalen
Polynoms gegeben.
ist vom Gaußschen Typ, wenn sie
für Polynome bis zum Grade 2n+1 exakt ist.
Zu vorgegebener Gewichtsfunktion w(x)
gibt es genau eine Gaußsche Quadraturformel.
Dabei sind die Stützstellen nicht mehr
frei wählbar, sondern durch die Nullstellen
des (n+1)-ten, bezüglich w(x) orthogonalen
Polynoms gegeben.
- Je nach Wahl der Funktion w(x) ergeben sich die nach den bekannten Klassen orthogonaler Polynome benannten Quadratur-Formeln: Gauß-Legendre, Gauß-Chebyshev, Gauß-Laguerre, etc.
- Prinzip aller Integration ist eine Schätzung
der Form