Der Lanczos-Algorithmus ist eines der einfachsten Verfahren zur Berechnung extremaler Eigenzustände großer, dünnbesetzter Matrizen, und kann immer dann zum Einsatz kommen, wenn der Speicherbedarf (aufgrund der Problemgröß) der limitierende Faktor ist.

Iterativ wird eine neue Basis des Hilbert-Raumes konstruiert, in der der Hamiltonoperator tridiagonal ist. Schon nach wenigen Schritten bilden die Eigenvektoren der (kleinen) tridiagonalen Matrix sehr gute Approximationen für die Eigenzustände der (hochdimensionalen) Ausgangsmatrix.

Als Kombination des Davidson-Verfahrens und eines alten Algorithmus von Jacobi wurde vor wenigen Jahren das Jacobi-Davidson-Verfahren vorgeschlagen, das sich insbesondere zur Berechnung vieler Eigenwerte auch im Innern Spektrums eignet. Mehr unter obigem Link.

Zur Berechnung von Spektraldichten, Korrelationsfunktionen, sowie zur Zeitentwicklung eignen sich Chebyshev-Polynome. Mehr Details in folgendem Vortrag.

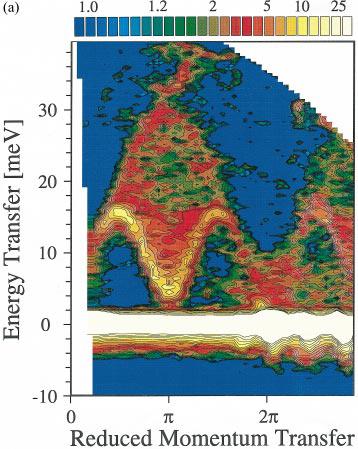
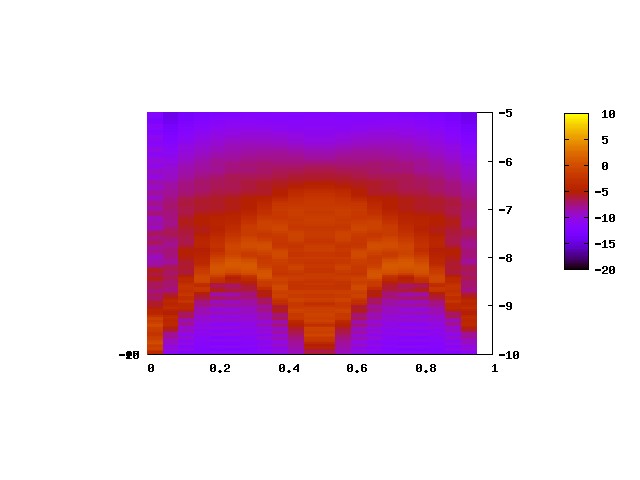
Neutronen-Streuung an CuGeO3, Arai et al. PRL 77, 3649 (1996)	Strukturfaktor des 1D Heisenberg-Modells (22 Spins)